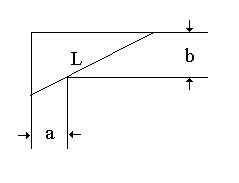
On appelle x l'angle (compris entre 0 et Pi/2) entre le mur du couloir de largeur b et la tige.
La longueur de la tige est alors f(x) = b/sin x + a/cos x, et on cherche le minimum de cette fonction.
La dérivée est : f ' (x) = (a*(sin x)^3 - b*(cos x)^3)/(sin x * cos x)^2.
Posons a=u^3 et b=v^3. Le minimum est obtenu pour x tel que u*sin x = v*cos x.
Il reste à calculer ce minimum : fmin = v^3/sin x + u^3/cos x = u*(u^2+v^2)/cos x.
Mais tan x = v/u, d'où cos x = u/sqrt(u^2+v^2) et fmin = (u^2+v^2)*sqrt(u^2+v^2) = (a^(2/3)+b^(2/3))^(3/2).

C'était un exercice qui traînait dans les manuels de première scientifique, avec des valeurs numériques pour a et b qui rendaient les calculs sympathiques (pas comme ci-dessus). Il était présenté comme un couloir de musée dans lequel on devait faire transiter un grand tableau en position verticale, et il fallait trouver la longueur maximale admissible du tableau.